Find the size of the earth by triangulation
This was first done by measuring the angle the sun makes at noon on a given day in two places miles apartFind the distance to Mars by triangulation, when at its closest point, using Earth diameter as a base.
. Two photographs of Mars against the night sky, one at dusk and one at dawn, give the angle. Use of the sine law, or a simple proportion, gives the distance with Earth’s diameter known.Find the distance to Mars in astronomical units.
By geometrical construction knowing the years of Earth and Mars.Divide the two distance measurements to get the length of the astronomical unit in miles.
Find the distances to the nearest stars by triangulation, using the astronomical unit as the base.
Make spectrographic studies of the stars to determine the different classes.
This is done by hooking a spectrograph up to the telescope to photograph the spectra of the star. Comparison with earthly elements gives knowledge of star’s composition.Make measurements of the observed or apparent magnitude of the stars with known distances.
Convert the magnitude to absolute magnitude, as if all starts were at the same distance.
Build the Herzsprung-Russell diagram, relating spectral class with absolute magnitude using the 700 or so known stars.
Measure the distance to any other star for which a spectrum and magnitude can be determined, especially in globular clusters, where all stars are nearly at the same distance.
Develop the period-luminosity relation for variable stars by studying variables in globular clusters.
Measure the distance to galaxies by measuring the period and magnitude of variable stars in them.
The magnitude and period of a stars can be determined much more easily than its spectrum, allowing the determination of very deep distances with bright variable stars.Measure the red shift of galaxies with known distances to develop the red shift and distance relation.
Find the size of the earth by triangulation
We do this by measuring the angle of the sun’s rays at two points with a known north-south distance . The shadow cast by two buildings would work.
The sun’s parallel rays are directly overhead for one place and cast a long shadow for the other. The angle the ray makes with the northern building is the same as the angle at the center of the earth.
We can make this proportion:
The angle is to 360 degrees as the distance is to 2 times PI times the radius of the earth.
With this, we solve for the radius.
R= 360*D/2*PI*A = 57.296 * D / A
Find the distance to Mars by triangulation, when at its closest point, using Earth diameter as a base..
We take a photo at dusk and another at dawn with Mars at its closest point to us. The skinny angle can be gotten knowing the focal length of the lens used and the distance between Mars points on the two photos.
The separation for one degree of angle = .01744 times the focal length of the lens.
With the angle known, and the diameter of the Earth, the triangulation equation gives the distance to Mars.
Find the distance to Mars in astronomical units.
This relates the distance to Mars to the distance to the sun, since the distance to Mars is easier to get.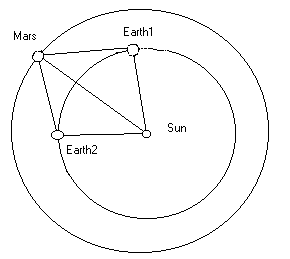
Mars has a year of 687 days. By measuring the angle between Mars and the Sun 687 days apart, we get a figure which we can get all the data for. The Earth makes the same angle each 687 days, but in different places on its orbit. In 43.5 days less than two years, Mars returns to the same place on its orbit, and Earth makes the same angle with it again. This makes the angle with Earth and the sun 43.5 divided by 365.25 times 360 or 42.87 degrees.
The rest of the angles vary somewhat depending on where on the orbit Mars is, but are easily measurable by timing the difference between the sunset and the setting of Mars.
With all the angles known, the relation of the sides can be gotten, with the distance from Earth to the sun being one Astronomical Unit.
Divide the two distance measurements to get the length of the Astronomical Unit in miles.
The distance to Mars in miles divided by the distance in Astronomical units gives miles per Astronomical Unit, or the distance to the Sun in miles.
All of these measurements are within the reach of the amateur astronomer, using small telescopes and standard tools ( like a camera and stopwatch).
Find the distances to the nearest stars by triangulation, using the astronomical unit as the base.
Just as we photographed Mars at dawn and dusk to get the parallax angle of Mars, so it is possible to do this with stars if the telescope is good enough.
The focal length must be very long for the angle to be large enough to detect, however, because the baseline is so narrow (8 light minutes is very small in comparison to a light year, and the nearest stars are more than 4 light years away).
It is possible to get a longer baseline than the astronomical unit, by using assumptions from the sun’s orbit. If we know the velocity and direction of the sun’s motion in the galaxy, we can get longer baselines by taking our pictrues more than six months apart-waiting for decades if necessary.
It is important, however, that the simple measures can be made, since the two different methods can serve as a check on one another.
Here are the distances on the plate for a degree of parallax with some different telescopes:
| 50mm camera lens | 0.872mm |
| 1000mm amateur’s telescope | 17.44mm |
| 200 inch Mt. Palomar | 292.36mm |
Here are the same distances for 1 second of parallax:
| 50mm camera lens | .000242mm (no lens can do this) |
| 1000mm amateur’s telescope | 0.00484mm (might be barely discernible) |
| 200 inch Mt. Palomar | 0.0812mm (not huge, but measurable with a microscope or magnifier) |
Our measurements are between 5 and .05 seconds of arc.
Though these values are small, they are measurable with relative ease, allowing pretty good repeatability of distance measures.
Make spectrographic studies of the stars to determine the different classes.
The classes are labeled in sequence, O,B,A,F,G,K,M, from the blue stars to the red. The sun is class G.It is possible to get an idea of the class with simple colored film and a clock drive. The star’s colors show up strongly in a long time exposure. A prism mounted over the objective of the telescope can give an indication of the class as well.
To really determine this, however, a spectrograph or spectrometer is used. Spectrographs can be arranged so that a photo of the star’s spectrum is made beside the spectrum of an element like hydrogen. In this way, the comparison is direct. This is the way red shifts are measured as well.
Make measurements of the observed or apparent magnitude of the stars with known distances.
The observed magnitude of a star can be gotten from measurement of the size of its apparent disk on a photo, or by comparing its brightness with that of an adjustable and calibrated artificial star in a beamsplitting eyepiece.
Convert the magnitude to absolute magnitude, as if all stars were at the same distance.
By knowing the distance of the star and its magnitude, the absolute magnitude or brightness can be found.
Build the Herzsprung-Russell diagram, relating spectral class with absolute magnitude using the 700 or so known stars.
This diagram, which I won’t reproduce, shows that stars have a pretty tight relationship between their spectral type and absolute magnitude.
There are four types of stars, white dwarfs, main sequence, giants, and supergiants with a tight relationship for each type. Once you know the spectral type and class, the absolute magnitude is pretty accurately known.
Here are some rough examples for main sequence stars:
| O | -10 |
| B | -5 |
| A | 0 |
| F | 2.5 |
| G | 2.5 |
| K | 5 |
| M | 10 |
These magnitudes would give useful distances. After all, it doesn’t matter much if we know a star is 24 or 25 light years away, as long as it is known that it is between 10 and 100. The H-R diagram gives results pretty close to plus or minus one magnitude step. It is interesting that it is possible to measure reasonable distances to stars with nothing more than the above table, a camera with color film, and a clock drive.
To do this, take a time exposure of the stars in question, determine the apparent magnitude ( having calibrated the film against known magnitudes earlier) by measuring the star image, determine the class from the color ( maybe using a prism over the lens), get the absolute magnitude from the H-R diagram or above table, and calculate the distance using the inverse square law for light. The equations involve squares, square roots or logarithms and therefore are beyond the scope of this simple description.
Measure the distance to any other star for which a spectrum and magnitude can be determined, especially in globular clusters, where all stars are nearly at the same distance.
All stars can now be given reasonable distances, simply by knowing the magnitude and color.
It can be objected that dust or gas between us and the star would give a wildly incorrect value for the magnitude and therefore for the distance. The amount of dust can be estimated, however, and even used as another way of measuring distance. The dust or gas doesn’t dim all parts of the spectrum equally.
Globular clusters are important here because the stars are all at nearly the same distance from Earth so there is a way to check the distance measurements for such stars. It is also possible to know the distance of stars which may not have a good example near Earth. The variable stars are the best examples here.
Develop the period-luminosity relation for variable stars by studying variables in globular clusters.
The cepheid variable stars are yellow super giant stars. Study of them in globular clusters revealed that the brighter the cepheid variable, the longer its period of fluctuation. Roughly, cephieds of 3 days period have absolute magnitudes between 0 and -1, while 50 day cephieds are around -3.5.
These are bright stars which can be seen for great distances-even in other galaxies.
Measure the distance to galaxies by measuring the period and magnitude of variable stars in them.
Measuring the period and apparent magnitude of cephied variables in another galaxy allows us to measure the distance to the galaxy since we know the absolute and apparent magnitude of the variable star.
Measure the red shift of galaxies with known distances to develop the red shift and distance relation.
The red shift of the spectrum is the movement of all the lines of the spectrum toward the red. It is measured by photographing the spectrum of the star beside the spectrum of the element in a “discharge lamp” (street lights are discharge lamps) here on earth. The lines for the element are the same and form a “fingerprint” pattern for the element. The stars will be moved toward the red, however.
The red shift is determined by the Doppler effect and is a measure of the motion of the star relative to us. If the star is moving toward us, the move is to the blue side, away from us, to the red.
The farther the galaxies are away, the more they are shifted to the red-the faster they are moving from us. This is the origin of the “big bang” theory of universe creation.
Using these tools, it is possible to give a pretty good guess for the distance of anything we can see!
Some people, seeing that astronomers measure distance in “light years”, think that measurement of the speed of light is somehow needed for knowledge of the distances. This is not true. None of the relations shown above depend on the speed of light. Studying doppler shifts does give other ways of measuring distances and so provides a check on the validity of results obtained, but many of these results would likely be the same even if the speed of light varied from one part of space to another!