This is an example of something useful: optical analysis of mirrors of different curvatures.
Mirrors for telescopes are ground of glass, polished, and figured to the correct curve.
The easiest curve is a section of a sphere, because grinding and polishing makes spheres automatically. Most optics use spheres wherever possible.
Unless a tlelscope mirror is of long focal length and small diameter, however, the image quality is poor for spheres.
A look at why follows the diagram:

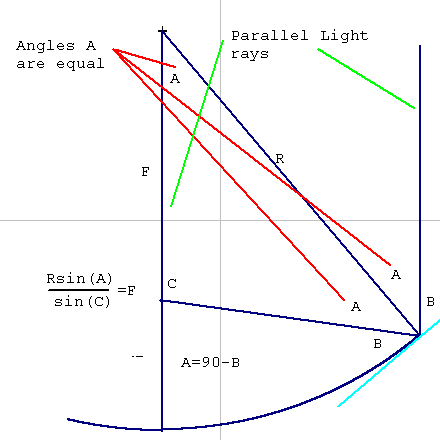
Here is a cross section of the spherical mirror with two rays from a distant star hitting it, one through the center of the sphere, and one a ways out on the surface. Because the star is so distant, the two rays are parallel
Draw a line from the center of the sphere to the intersection of the outer ray and the surface. Draw the tangent to the circle at that point (the tangent touches the circle at only one point and is perpendicular to the radius line).
The light from the star will be reflected as if the tangent line were a flat mirror. The angle,B, between the ray and the tangent equals the angle,B, between the reflected ray and the tangent.
A = 90-B
Because the two rays are parallel, the angle at the center of the sphere also equals A.
We have a triangle with three known angles ( A,A, and 180-2A), and a known side (R).
The sine law will find the unknown side:
| R | F | |
| ------------- | = | -------- |
| sin(180-2A) | sin(A) |
Multiplying both sides by sin(A) gives F by itself on the right:
| Rsine(A) | ||
| ------------- | = | F |
| sin(180-2A) |
Here are some values of F where the radius of the sphere is 128:
| Angle A | F |
|---|---|
| 45 | 90.5097 |
| 10 | 64.9873 |
| 1 | 64.0098 |
| .1 | 64.00011 |
| .01 | 64.000087 |
As you can see, the smaller angles ( which are longer focal lengths and smaller mirrors) give values closer and closer to half the radius. This error in focus is called spherical aberration.
Notice that the way we derived this is by building an isoceles triangle and using the sine law on it. This is a very powerful way to solve problems.
Since the sphere doesn't make the most perfect mirror, we can try the parabola.
The parabola is a little more complicated because we don't have a radius, and the tangent line continually varies. It is not impossible, however, using some simple concepts and the calculus formula for the slope of a line tangent to the curve.
The slope of the tangent to a parabola ax2 is 2ax. This is just using the slope of axn as naxn-1..
If a sphere has radius R, the parabola which is closest to it in shape has the formula:
| x2 | ||
| y | = | ------ |
| 2R |
The formula for the slope of the tangent (S) is:
| x | ||
| S | = | --- |
| R |
Here is a diagram:
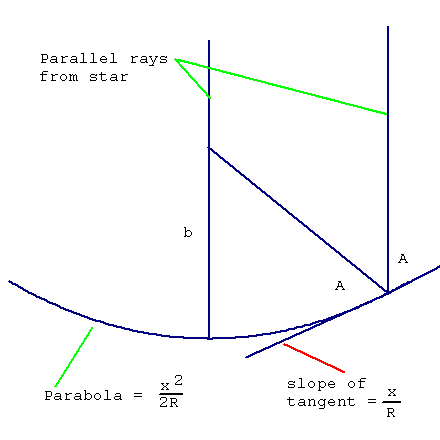
Here is how the formulas for the raytrace are derived:
First get the slope of the tangent in degrees to calculate angle A ( the complement of the slope):
D = arctan(S)
A=90-D
The slope, in degrees, of the reflected line is D-A. The slope of the line (M) is the tangent of the angle in degrees..
M= tan(D-A)
The complete formula for the line is y = Mx +b, where M is the slope and b is the y value when x = 0. Since the ray comes to a focus ( intersects the axis ray) at the point where x = 0, b is the hieght of the focus of the mirror.
y=Mx+b
Subtracting Mx from both sides gives:
y-Mx = b.
Here are some values where the radius of the sphere is 128:
| x | y | slope | angle A | M | b |
|---|---|---|---|---|---|
| 1 | .0039063 | .0078125 | 89.552386 | -63.996095 | 64.000001 |
| 2 | .015625 | .015625 | 89.104826 | -31.992188 | 64.000000 |
| 3 | .0351563 | .0234375 | 88.657376 | -21.321614 | 63.999999 |
The accuracy of focus is obviously much better. In fact, the tiny errors are introduced by my calculator.
This shows the power of a few simple tools and concepts to solve real world problems.
This problem was solved when the calculus was first invented. This solution is widely known. Many of the results of the calculus were arrived at centuries ago so that modern man just sees the result and wonders why the calculus is necessary. Feeling comfortable with the results and methods of calculus, however, has become a dividing line between those who can do and those who are done to as technology expands into all human spheres.
The amount of calculus needed to solve an enormous number of problems is very little. In the above case, the calculus quickly got us a formula for a straight line, and all other work was done in the realm of straight lines. That is the main power of calculus--to simplify a complex problem to one of straight lines and simple areas.
I hope you liked this example.