This is about the math you can love. This is math you can actually use.
Live and breathe this stuff and your life can change.
This is the math which is every human's birthright and one of mankind'smost powerful celebrations.
Here are a some principles I've used in writing this:
In reading this, don't skip any of the words. That way, you won't miss anything because you thought you knew it.
If something doesn't make sense, reread it.
If it still doesn't make sense, put the book down until the next day.
If it still doesn't make sense, find one of the ten thousand books written on that subject which explains it better, or get one of your friends to explain it--over and over till you get it.
Knowing the math in this book is part of your birthright as a human. Don't let anyone cheat you out of it.
Math begins with the point. A point is a location in space. We represent them with dots, arrows, or crossed lines.

We usually need two lines to define a point's location. In fact, an arrow is really just three crossed lines ending in a point.
We need two straight lines to determine a point. How do we get straight lines?
A straight line is the intersection of two plane surfaces. Two lines determine a plane surface and two plane surfaces determine a line.
One way to get a reasonably straight line in the real world is to stretch a string between two points.
Accurate straight lines in the real world are made by intersecting two accurate plane surfaces.
Accurate plane surfaces are made by grinding three surfaces together until they all fit each other. These are usually made of cast iron, glass, or granite.
Here's how that works ( for those really interested):
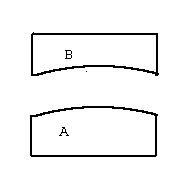
If two surfaces (call them A and B) fit one another, and they are not plane then one ( call it A) has a convexity to match the other's concavity (B).
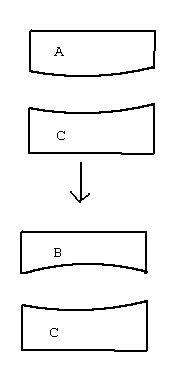
The convex surface of A will make a concavity on surface C and surface B will not fit C ( concave to concave).
The concave surface of B will make a convexity on C and A will not fit C ( convex to convex).
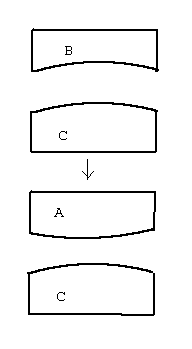
Therefore, if A,B, and C all fit the surface must be a plane.
Believe it or not, every bit of high tech stuff in the whole world starts on that plane surface. None of it happens without it.
Three lines intersecting form a triangle. Triangles are the most basic and most useful figure. They are rigid. Once you fix two sides and their common angle, or two angles and their common side, or the lengths of the three sides, the triangle is formed and cannot change shape and remain a triangle.
If you have a square or rectangle of metal, and cut the middle material out, it becomes flimsy. A triangular piece with the middle material cut out can be as strong as the original piece.
Types of Triangles
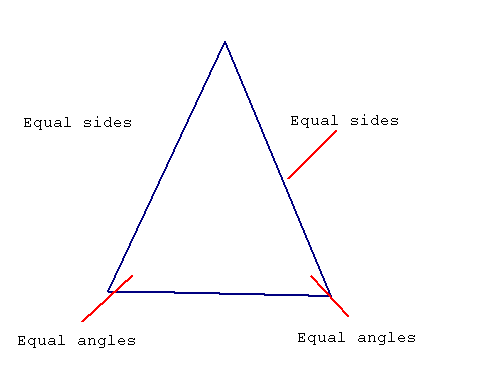
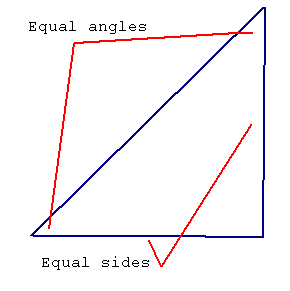
The most useful triangles are the isoceles, right, and equilateral.
Isoceles means equal sided and refers to a triangle with two equal sides and angles.
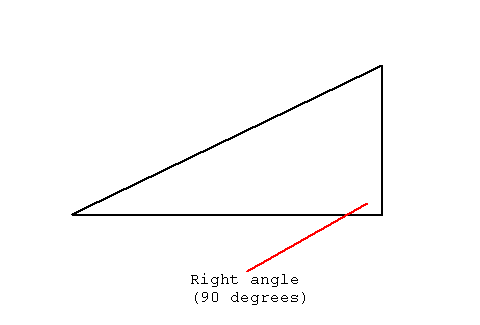
Right means right as in upright. The right triangle has a right angle in it. The right angle is the angle we make with the ground. It's also the angle a string makes with the ground when it's suspended by a weight. There are two right angles in a straight line and the sum of all the angles in a triangle seems to be two right angles or the angle of a straight line. A right angle is 90 degrees. A straight line is 180 degrees.
Equilateral means equal sided. All sides and angles are equal. The angle is one third of 180 or 60 degrees.
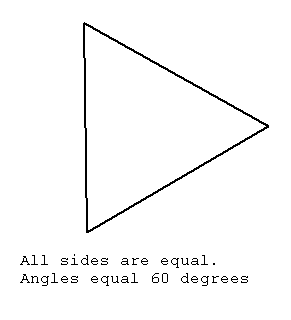
An isoceles right triangle has angles of 90, 45 and 45 degrees.
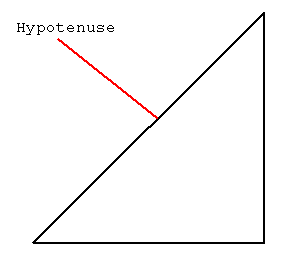
One other weird word used with triangles is the word "hypotenuse". The hypotenuse is the longest side in a right triangle.
We can get another useful triangle from the equilateral by drawing a line from one corner to the middle of the other side, making two right triangles:
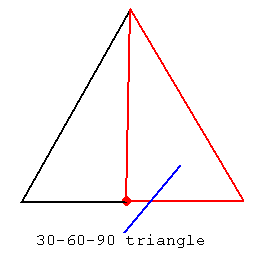
These two new triangles are called the 30-60-90 triangles.
Most of the work people have done with triangles has been done with the 45-45-90, the 30-60-90, and the equilateral.
Draw a right triangle and form the squares on its sides:
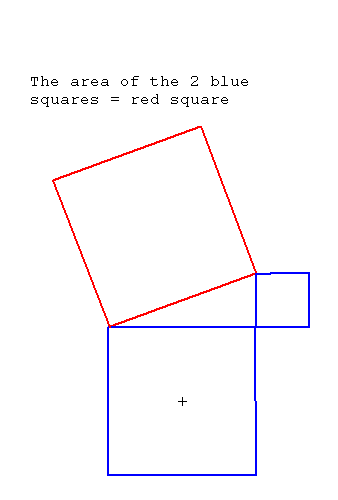
The area in the square on the longest side (the "hypotenuse") is equal to the sum of the areas in the other two squares.
For example, take a right triangle with sides 3 , 4 , and 5.
This theorem is thousands of years old and serves as the basis for a lot of mathematics.
The right isoceles triangle with short sides of 1 has a hypotenuse of the square root of two or about 1.414.
The 30-60-90 triangle has sides of 1,2 and the square root of 3 or about 1.732
These results are very useful since the triangles are used so often.
Triangle Area
The formula for the area of a triangle is to multiply one-half the size of the base by the height.
Polygons are many sided figures ( from the Greek, pollos, many, and gonos, side). They are figures which have more sides than a triangle.
The first group are the quadrilaterals, or four sided figures.
The special ones are:
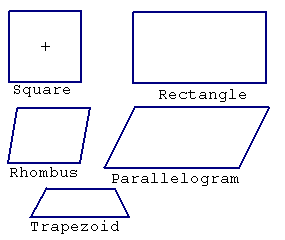
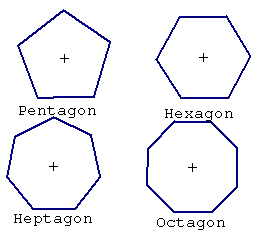
In the polygons with more sides, there is really only interest in the figure with all sides of equal length.
Any polygon can be broken up into triangles to find things like the area, the way to construct it, and so on, like this:
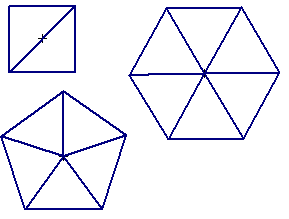
Always try to reduce your structure to its triangles, since this will make them simple to work with, though, like all such processes, it reduces the mystery.
A circle is all the points that can be drawn at the same distance from a single point called the center. They are usually drawn with a compass. In the real world, lathes are designed to make circles of great accuracy.
Circles are useful because they can be used to measure things, as in the famous ruler and compass constructions.

We are always surrounded by things. In my mind I can collect these things into groups or collections--all the shoes in my house, or all the split peas. Any collection can be identified by its size if I have a name for each size.
A number system is a way of naming each size collection. By having a system of numbers, we can make a name for any size we want.
If we have a number, and we add one to it, we must be able to name the new number.
In the decimal system, we have the numbers one through nine, the numbers ten through ninety, the name hundred, the name thousand, the name, million, the name billion, and the name trillion. This is a total of 23 names for numbers which in diffrent combinations can name every size of collection from one to much farther than I care to contemplate--say the number of atoms on every beach in the world, or the number of stars in the known universe.
This is how it works:
Counting is adding one to each number in succession while moving the collection one by one from one pile to another.
When you have counted to nine, you say ten and start over until you reach nineteen (I've ignored the quaint words eleven, twelve, etc. ) then you say twenty and start over until twenty-nine, and so on until you reach ninety-nine.
You then say one hundred and start over.
When you get to ten hundred, you say one thousand and start over.
When you get to one thousand thousand, you say one million.
When your children get to one thousand million ( in the United States), they say one billion.
When your children's children's ...(this goes on for four hundred generations)...children's children get to one thousand billion, they say one trillion.
We can always add one and name the new number. Our children's...children can always add one and name a new number.
We call this system of numbers the NATURAL NUMBERS.
We reverse an addition by subtracting.
Can we always subtract and name a new number? Not if the number is one.
To solve this we have a number called zero which stands for no things.
We call this system of numbers ( with the zero) the WHOLE NUMBERS.
What if we subtract from zero? When this has happened in my bank account before, I changed from black to red ink or put paraentheses,like (204.30), around the number to indicate that the collection that was in my pile is now in someone else's pile. Another way to indicate this is to put a minus sign before the number, like -204.30.
We call numbers with a minus sign NEGATIVE NUMBERS, those without are the POSITIVE NUMBERS.
We call the system of numbers with positive numbers and negative numbers the INTEGERS.
A faster way to count numbers is to group everything in equal clumps first:
Then we count all the clumps and multiply by the size of the clump.
To multiply, you memorize some tables and activities or use a calculator.
If a machine can do all the clumping for you, then this method of counting really flies. For example, a machine puts 12 eggs in each carton. To find the number of eggs, count the cartons and multiply by 12.
You can always multiply and get a nameble new number in the integers.
Here's how to handle the minuses:
A positive number ( no minus siqn) multiplied by a positive number yields a positive number.
A negative number (with a minus sign) multiplied by a positive number yields a negative number.
A negative number multiplied by a negative number yields a positive number.
Note that by these rules a number squared ( multiplied by itself) is always positive.
You reverse an addition by subtracting, you reverse a multiplication by dividing.
You can't always divide and name the number in the system of integers.
To get to nameble numbers again, you need FRACTIONS.
Fractions are unique names for numbers which cannot be divided. If I divide nine by three the result is three ( or, in fraction form, three oneths).If I divide three by nine the result is three nineths. If I divide twenty-two by two hundred sixty-five, I get twenty-two two hundred sixty-fifths.
We also have a special way of naming fractions in decimals: The decimal point. In the number 123456.789 , each number going left is ten times larger than its nieghbor. To the right of the decimal point, the fractions start. .789 is seven tenths plus 8 hundreths, plus 9 thousanths or seven hundred eighty-nine thousanths.
Fractions can be expressed as a top and a bottom part ( numerator and denominator, to be technical).
There are two tricks which tame fractions. Converting them to decimals, and changing the numbers.
To convert to decimals, first multiply the top of the fraction by a ten enough times to make it larger ( maybe even a lot larger ) than the bottom.
Next, divide the bottom into the large top number normally.
Finally, divide by ten the same number of times you multiplied before.
This is simple since multiplying by ten means moving the decimal point to the right, and dividing moving to the left.
The second trick comes from noticing that you can always multiply or divide the top and the bottom by the same number and the fraction is unchanged.
Calculators make fractions a lot easier to deal with.
Numbers expressed as fractions are called RATIONAL NUMBERS.
Multiplication allows us to deal with big numbers easily, but a special form of multiplication makes even bigger numbers easy. This is called raising to a power. The word power is in there because people feel powerful when they do this.
Multiplication is repeated addition. A number is added to itself a number of times.
Raising to a power is repeated multiplication. A number is multiplied by itself a number of times.
The little number 6 in 10 6 is called the exponent and expressing the number in this form is called the exponential form
We can also divide sucessively:
Here is the short version:
| 1,000,000 | 106 |
| 100,000 | 105 |
| 10,000 | 104 |
| 1000 | 103 |
| 100 | 102 |
| 10 | 101 |
| 1 | 100 |
| .1 | 10-1 |
| .01 | 10-2 |
| .001 | 10-3 |
| .0001 | 10-4 |
| .00001 | 10-5 |
| .000001 | 10-6 |
Scientific Notation
It is obvious that the easy way to express big powers of ten is as 10x.It would be nice to use this ability to express any number.
We can do this by breaking the number into two parts,a power of one part and a power of ten part.
In this scheme, 1 is 1 times 100, 2 is 2 times 100,10 is 1 times 101,20 is 2 times 101.
Here are some examples:
| 3,260,000 | 3.26 times 106 | 3.26 X 106 | 3.26E6 |
| 326,000 | 3.26 times 105 | 3.26 X 105 | 3.26E5 |
| 32,600 | 3.26 times 104 | 3.26 X 104 | 3.26E4 |
| 3260 | 3.26 times 103 | 3.26 X 103 | 3.26E3 |
| 326 | 3.26 times 102 | 3.26 X 102 | 3.26E2 |
| 32.6 | 3.26 times 101 | 3.26 X 101 | 3.26E1 |
| 3.26 | 3.26 times 100 | 3.26 X 100 | 3.26E0 |
| .326 | 3.26 times 10-1 | 3.26 X 10-1 | 3.26E-1 |
| .0326 | 3.26 times 10-2 | 3.26 X 10-2 | 3.26E-2 |
| .00326 | 3.26 times 10-3 | 3.26 X 10-3 | 3.26E-3 |
| .000326 | 3.26 times 10-4 | 3.26 X 10-4 | 3.26E-4 |
| .0000326 | 3.26 times 10-5 | 3.26 X 10-5 | 3.26E-5 |
| .00000326 | 3.26 times 10-6 | 3.26 X 10-6 | 3.26E-6 |
Roots
102, or ten squared, is 100. Ten is the square root of one hundred.
103, or ten cubed, is 1000. Ten is the cube root of one thousand.
The easiest way to express a root is as a fractional exponent: the square root of 100 is 1001/2.
Roots are sometimes difficult to evaluate, requiring a calculator or table. Some can never be perfectly calculated and must be rounded off.
Here are some common roots (rounded off where needed):
| 1000,0001/2 | 1000 |
| 10,0001/2 | 100 |
| 1001/2 | 10 |
| 101/2 | 3.162... |
| 91/2 | 3 |
| 41/2 | 2 |
| 31/2 | 1.732... |
| 21/2 | 1.414... |
| 11/2 | 1 |
The three dots after some numbers indicate that the number continues on forever.
Evaluating formulas
To evaluate a formula, say f=3x where x = 5, substitute the number for the letter,f=3(5), and multiply (where a number is right beside a letter, that means to multiply) to get 15.
To evaluate a formula, say f=3x2 where x = 5, substitute the number for the letter with its exponent, f=3(52). Do the calculation inside the parenthesis first-- 52=25--then multiply--3 times 25 = 75.
,p.To evaluate something really complex, like f=10((3+5)x2) where x=5, use the following order:In our example,
The Linear Formula
A linear formula is one in which none of the letters is raised to a power. It is called linear because a graph of the formula is a straight line.
Take y = 3x. this means that every y value is three times the x value.
First, make a table with some reasonable x values (say, between -5 and 5) and the associated y values:
| x | y |
|---|---|
| -5 | -15 |
| -4 | -12 |
| -3 | -9 |
| -2 | -6 |
| -1 | -3 |
| 0 | 0 |
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
| 4 | 12 |
| 5 | 15 |
If we plot this with x as the horizontal and y as the vertical, we get a graph of a straight line like so:
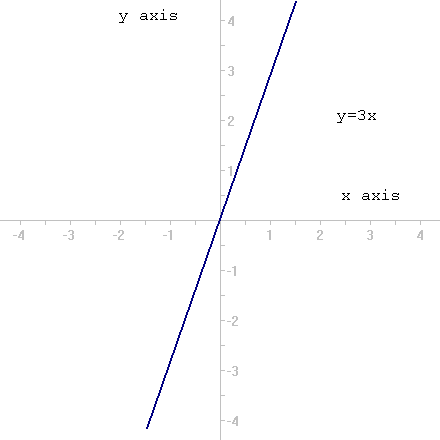
In all linear formulas, we say that y is proportional to x.
The linear formula with constant
The most important form of the linear formula is the simplest:, a=kb, or a equals k times b, where k is a number. Our y=3x example is of this sort. The k is called the constant ,because, as a number, it can only have one value. The letters are called variables because their value varies.
Here are some examples of such formulas:
These formulas are the lifeblood of analysis for many disciplines.
The linear formula with all variables
The next type of the linear formula has all variables, as in a=bc. Here all a is proportional to either b or c.
We can manipulate this formula to get a, b, or c by itself:
Dividing both sides by c:
| a | b | c | |||||
| -- | = | -- | |||||
| c | c |
Since c divided by itself is 1, and b times 1 is b, we simplify:
| a | |||||||
| -- | = | b | |||||
| c |
The result is that b is equal to a divided by c.
To get c by itself from:
Dividing both sides by b:
| a | b | c | |||||
| -- | = | -- | |||||
| b | b |
Since b divided by itself is 1, and c times 1 is c, we simplify:
| a | |||||||
| -- | = | c | |||||
| b |
The result is that c is equal to a divided by b.
Proportions
Another way to look at the linear formula is as a proportion. The phrase that tips you off to the use of a proportion is "is to". The sentence we use for proportions is "a is to b as c is to d".
Here are a few examples:
Here are these examples in algebraic form:
| C | 12.011 | |||||||
| -- | = | --------- | ||||||
| O | 15.9994 | |||||||
| De | 2(pi)Dem | |||||||
| ---- | = | --------- | ||||||
| A | 360 | |||||||
| D | 1 | |||||||
| -- | = | --------- | ||||||
| C | 3.1415... | |||||||
Expressed in this way, the linear formula is often easy to conceptualize. If you can say the word problem as a sentence with is to and as, the proportion is obvious. Both the 3 number form of the formula and the proportional form say the same thing, and can always be converted from one to the other. In order to solve the problem we need to make a formula with only one variable on one side--as in the 3 number form.
Converting from One Linear Form to Another
To convert from the proportion, first cross multiply, getting the proportion as ad = bc, then divide by whichever one is not wanted on a side.
Here is cross multiplication in some detail:
Given:
| a | c | |||||||
| -- | = | -- | ||||||
| b | d | |||||||
Multiply a by d and b by c, to get ad = bc.
| a | c | |||||||
| -- | = | -- | ||||||
| b | d | |||||||
I won't prove that this works ( though the "proof" is to multiply both sides by b and d and simplify), but if you memorize this you are well on your way to mastering a lot of math and science.
Once we have the form, ad = bc, we divide by what's not wanted.
To get a by itself, divide by d:
| ad | bc | |||||||
| --- | = | --- | ||||||
| d | d | |||||||
| bc | ||||||||
| a | = | --- | ||||||
| d | ||||||||
Here is the carbon monoxide example solved for carbon:
| C | 12.011 | |||||||
| -- | = | --------- | ||||||
| O | 15.9994 | |||||||
| 12.011(O) | ||||||||
| C | = | ----------- | ||||||
| 15.9994 | ||||||||
Here is the carbon monoxide example solved for oxygen:
| C | 12.011 | |||||||
| -- | = | --------- | ||||||
| O | 15.9994 | |||||||
| 15.9994(C) | ||||||||
| ------------ | = | O | ||||||
| 12.011 | ||||||||
Similar Triangles
A very large number of the problems involving proportions arise out of triangles which are the same shape, but different size. These triangles are called similar.
The easiest way to make them is to draw two lines out from a point, and cross them with parallel lines:
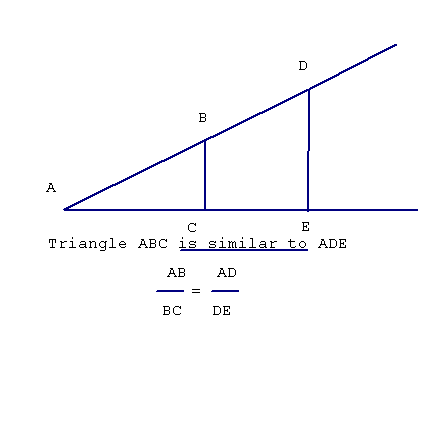
In this example, I find the height of a building by making similar triangles with sticks of known height:

I can do this by lining up the tops of the sticks and the building, then sighting back along the sticks to find the point of the triangle on the ground. Measuring the distance from that point to one stick, from that point to the building, and the height of the stick, gives me all the numbers needed for the proportion
The Mean or Average
The mean or average is a single number which represents a group of numbers. The collection of data often results in more numbers than can be interpreted. Taking the mean gives a single number from the mess.
To get the mean of a group, add all the numbers together and divide by the number of numbers.. If I have 3,4,5, and 6, I add to get 18, and divide by 4 to get 4.5.
Here it is again:
| Index | Value |
|---|---|
| 1 | 3 |
| 2 | 4 |
| 3 | 5 |
| 4 | 6 |
| Sum | 18 |
| Divide by | 4 |
| mean | 4.5 |
In this case we counted the numbers with an index and divided the sum by the last index to get the mean. Just count the number of numbers an use that for the divisor.
The Deviation
The mean is a good way to measure a group of numbers, but it doesn't give as much information as we often need. The second most useful number is the deviation.
If I use the numbers 3,4,5,and 6, the mean is 4.5. I can also get the same 4.5 with 1,2,5, and 10.
Here are some more examples:
| Index | Value | ||
|---|---|---|---|
| 1 | 3 | 1 | -250 |
| 2 | 4 | 2 | 250 |
| 3 | 5 | 5 | 0 |
| 4 | 6 | 10 | 4.5 |
| Sum | 18 | 18 | 18 |
| Divide by | 4 | 4 | 4 |
| mean | 4.5 | 4.5 | 4.5 |
To get the simple deviation, subtract the mean from the number:
| Index | Value | Deviation |
|---|---|---|
| 1 | 3 | -1.5 |
| 2 | 4 | -.5 |
| 3 | 5 | .5 |
| 4 | 6 | 1.5 |
| Sum | 18 | 0 |
| Divide by | 4 | 4 |
| mean | 4.5 | 0 |
The average of the deviation in this case is zero. This is not very useful, since the actual average error from the mean is one. Simple deviation is very seldom used.
Standard deviation takes the deviation of each number, squares it, averages the squares, and takes the square root of the average. This gets rid of the minus signs.
Here's an example:
| Index | Value | Deviation | Square |
|---|---|---|---|
| 1 | 3 | -1.5 | 2.25 |
| 2 | 4 | -.5 | .25 |
| 3 | 5 | .5 | .25 |
| 4 | 6 | 1.5 | 2.25 |
| Sum | 18 | 5 | |
| Divide by | 4 | 4 | |
| mean | 4.5 | 1.25 |
The square root of 1.25 is 1.11803...
Here are the standard deviations for the other examples:
| Index | Value | ||
|---|---|---|---|
| 1 | 3 | 1 | -250 |
| 2 | 4 | 2 | 250 |
| 3 | 5 | 5 | 0 |
| 4 | 6 | 10 | 4.5 |
| STD | 1.118 | 4.041 | 204.137 |
The standard deviation and the mean together give a very good representation of the group of numbers. Averages are used everywhere.
Here is one more example. A teacher gives a 30 question test to 5 students. The average student will get a "C". One standard deviation above will get a "B" and two STD's above will get an "A".
Here is the list:
| Index | Score | Grade |
|---|---|---|
| 1 | 5 | F |
| 2 | 14 | C |
| 3 | 15 | C |
| 4 | 20 | B |
| 5 | 17 | C |
| Mean | 14.2 | |
| Std | 5.04 |
The advantage here is that performance is based on the whole group's comprehension, and therefore, minimizes the teacher factor. The standardized tests (SAT,GRE, MPPI,etc.) are given to large populations and averaged to calibrate the test before it is given to an individual. Such tests give an indication of an individual's position in the population.
The right triangle is the most useful of all the triangles. The pythagorean theorem allows us to measure any side if two of the sides are known, but fails to help if all that can be measured is one side and the angles.
If something is too big or too inaccessible to measure, the angles may be all that can be gotten.
One way to deal with this if the accuracy is not too great, is to draw a scaled down picture of the triangle and measure the parts. The distances are multipled by the scale factor to get the actual sizes.
First, we need a standard way of naming the sides of a right triangle.
We are already familiar with the hypotenuse, or longest side.
The shorter sides are interchangeble and cannot be given unique names. Since we are measuring angles, however, we can refer to them in relation to the angle we measure.
The side which makes up part of the angle we measure we call the adjacent side.
The side which isn't part of the angle is the opposite side.
Here is a picture:
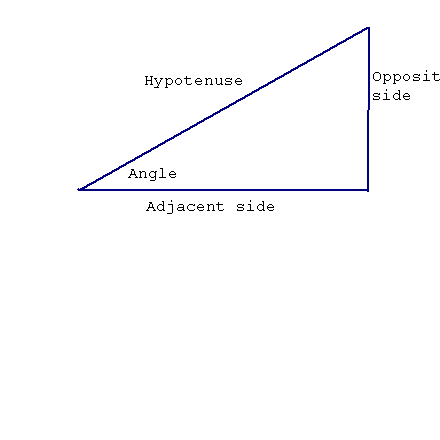
We will make this simpler by using O,A, and H.
What is needed is a formula to relate a side to an angle.
For any angle there is a constant which relates two of the sides.
These constants are found in Trig tables or are calculated by scientific calculators.
The three which we are going to look at are the sine, the cosine, and the tangent.
The Sine of an angle times the hypotenuse equals the opposite side.
The Cosine of an angle times the hypotenuse equals the adjacent side.
The Tangent of an angle times the adjacent equals the opposite side.
For and angle a:
An easy way to remember this is to think of the "famous mystical chinese philosopher" SHO CHA TAO. I won't go into the one about the "famous indian chief".
These three formulas plus the pythagorean theorem will allow you to do about all that you would want in measuring right triangles.
Measuring other triangles
With one exception, which I am about to give, measuring other triangles using trigonometry requires formulas which are hard to memorize. If you ever think you might need one, look it up in a book.
The one exception is the formula for sines. For any triangle, the sine of an angle divided by it's opposite side is the same for all sides.
Here is the formula:
| Sine(A) | Sine(B) | Sine(C) | ||||||||||||||
| -------- | = | -------- | = | -------- | ||||||||||||
| a | b | c | ||||||||||||||
Where the capital letters are the angle and the small letters are the side opposite the angle.
The cross multiplied way fo expressing the sine law is:
bsine(A) = asine(B)
For any two sides.
The formula y = 3x is often called a linear function. Any function can be thought of as a program for a computer where a one number goes in ( in this case x) and another number comes out (y or 3 times x).
The sine, cosine, and tangent are functions where the number for the angle goes in and the fraction for the sides comes out.
Most calculators and computers work with functions--just type the number in and press the button to get its function value.
The important functions are the linear, the square, the sine, the cosine, the tangent, the exponential, and the logarithmic.
We have looked at the linear, sine,cosine,and tangent.
The square is a function of the form y = ax2.
This function, when graphed, produces a curve called the parabola:
Here is our table of x and y for the graph of y=x2:
| x | y |
|---|---|
| -5 | 25 |
| -4 | 16 |
| -3 | 9 |
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |

Often, when data does not fit a linear function, it will fit some parabola.
The Logarithmic and Exponential Functions
The logarithmic and exponential functions are inverses of each other. We usually get the logarithm by entering an number in a calculator and pressing the "LOG" key. We get the exponential by entering a number in a calculator and pressing the INV and LOG keys.
The great thing about a logarithm is that we can multiply two numbers by adding their logarithms and converting the result with the exponential function..
Here are a couple of examples:
| Number | Log | Number | Log | Sum | Inverse Log |
|---|---|---|---|---|---|
| 2 | .303103 | 3 | ..477121 | .778151 | 6 |
| 4 | .60206 | 5 | .69897 | 1.30103 | 20 |
This was very useful before calculators and computers, since a table of logs could be used to multiply. The trick is not so useful now, but it leads to something which is still useful--getting any power or root quickly.
Since a power of a number is just a repeated multiplication, we can raise a number to a power by multiplying the logarithm by the exponent and converting the result with the exponential function.
Here are a some of examples:
| Number | Log | Exponent | Exponent times Log | Inverse Log |
|---|---|---|---|---|
| 2 | .303103 | 2 | .606206 | 4 |
| 4 | .60206 | 2 | 1.212412 | 16 |
| 5 | .69897 | .5 (square root) | .349485 | 2.236068 |
| 5 | .69897 | .2(fifth root) | .139794 | 1.37973 |
| 1.37973 | .139794 | 5 | .69897 | 5.000006 |
| 5 | .69897 | 5 | 3.49485 | 3125 |
Now you have a quick way to get the fifth root of five or the 55th root of 37( if you should ever need it).
Rate of change and Area
In our function y=3x, y changes 3 for every x. We can say that the rate of change of y with respect ot x is 3. This rate of change is also called the slope.
Finding the rate of change of a linear function is easy. We will introduce a couple of formulas to find it for some more complex functions in a moment.
Finding the areas and volumes of things is another useful thing to do.
The interesting thing here is that the rate of change of a function and the area under the curve are inverse operations--one undoes the other.
The rate of change of y=3x is 3.
The rate of change of y=x2 is 2x..
The rate of change of y=axn is anxn-1 ..
The area under the line of y=x between 0 and x is x2 divided by 2.
The area under the curve of y=x2 between 0 and x is x3 divided by 3.
The area under the curve of y=axn between 0 and x is axn+1 divided by n+1.
A couple more:
The rate of change of the sine is the cosine.
The rate of change of the cosine is the negative of thesine.
You have now gotten the world's shortest ( and,I think, most useful) calculus course.
Here is a real world example of use of some of this math.